



皆さんこんにちは。横浜国立大学フォーミュラプロジェクト 駆動設計担当です。今日のテーマは、以前ご紹介した「歯車」の続きです。前回は、歯車のあれこれということで、概要や歴史、種類とそれに対する用途についてご紹介しました。今回は、歯車の中でも最も一般的な、平歯車の諸計算式についてご紹介します。
歯車は恐らく、多くの方が馴染みのないものかと思いますが、実は身の周りの機械のあらゆるところで活躍しています。自動車においても、トランスミッションやファイナルドライブをはじめ、パワーウインドウの駆動部分や、ワイパーの駆動部分にも使われています。写真は弊チームマシンと搭載されているファイナルドライブです。

弊チームマシン

ファイナルドライブ
歯車の、歯の輪郭曲線を歯形曲線といいます。現在使用されている歯車の多くの歯形曲線はインボリュート曲線であり、歯形曲線がインボリュート曲線である歯車のことをインボリュート歯車といいます。インボリュート曲線とは、円筒に巻いた糸を引張ながらほどいていくときの糸の先端の軌跡が描く線のことです。インボリュート曲線を描くには、空き缶などの円筒形のもの、鉛筆、糸を用意して、以下のような手順で描くことができます。
手順①円筒の外周に糸を巻いて、その糸の先に鉛筆をつける。
手順②鉛筆で、その糸をゆるませないように、糸がピンと張った状態を保ちながほどく。
糸を巻き付けた円筒の円を、基礎円といいます。この基礎円の大きさが変化すると、インボリュート曲線も変化します。
インボリュート歯車が、歯車の中で大部分をしめる理由としては、製作が容易なため安価であること、互いの歯車軸の中心間の距離が多少変動しても、正確にかみ合うこと、1つの工具で、種々の歯形を歯切りすることができることなどが挙げられます。
多くの歯車は、基本的にモジュール、圧力角、歯数、歯幅、ねじれ角の5つの項目を設定することで、その形状を決定することができます。今回は、最も一般的な平歯車を対象に紹介します。
(1) モジュール:モジュールとは、歯の大きさを表す指標の値です。モジュールの値が、大きくなるほど、歯の大きさも大きくなります。
(2) 圧力角:圧力角とは、歯面の1点において、その半径線と、歯形への接線とのなす角度のことです。現在では、一般的に圧力角は20°とされています。
(3) 歯数:歯数とは、歯の枚数のことです。
(4) 歯幅:歯の軸断面内での長さです。
(5) ねじれ角:はすば歯車は、歯すじがつるまき線状にねじれています。ねじれ角とは、この時のつるまき線と、円筒の母線とのなす角度のことです。ねじれ角は、一般的に10°から30°の間の値が、用いられています。
諸計算式の紹介の前に、平歯車の用語について紹介します。
・基礎円:インボリュート歯形の、インボリュート曲線が作られる基礎となる円のこと。
・歯先円:円筒歯車の歯先を含む円のこと。
・歯底円:円筒歯車の歯底を含む円のこと。
・基準ピッチ円(基準円):基準ピッチを歯数倍した長さの円周をもつ円のこと。
・ピッチ点:1対の歯車のピッチ円の接点のこと。
・接触点:1対の歯車が接触している点のこと。
・作用線:1対のインボリュート歯車の接触点の軌跡のこと。
・かみ合い長さ:インボリュート歯車において、接触点の軌跡のうち、実際にかみ合いが行われる部分の長さのこと。
・頂げき:歯車の歯先円から、それとかみ合う歯車の歯底円までの距離のこと。
・バックラッシ:1対の歯車をかみ合わせたときの、歯面間の遊びのこと。
・歯面:歯車のかみ合い面のこと。
・歯溝:歯の溝の部分のこと。
・歯すじ:歯面とピッチ面との交線のこと。
・歯先面:歯先での歯幅方向の面のことで言い換えると外周面ともいえる。
・円ピッチ:ピッチ円上で計った、隣り合う歯の対応する部分間の距離のこと。
・法線ピッチ:基礎円の円周長さを歯数で割った値のこと。
・全歯たけ:歯の全体の歯たけ方向の長さのこと。言い換えると歯の高さのこと。
・歯末のたけ:歯車のピッチ円から歯先円までの距離のこと。
・歯元のたけ:歯車のピッチ円から歯底円までの距離のこと。
歯車の各寸法を計算する上で、はじめに基準ピッチ円、歯先円、基礎円の直径を算出します。この3項目は、他の各寸法を算出する際にたびたび必要となります。歯車の諸元を設定した後は、これらを算出する。計算式を表1に示します。

※z:歯数、m:モジュール
上記の3項目を算出したら、次に他の各寸法を算出していきます。円ピッチは、基準ピッチ円の円周を歯数で割ったものです。これは、基準ピッチ円上において、歯の位置から、次の歯の同じ位置までの円弧の長さを示しており、次式のように示されます。また、モジュールは、次式のように示すことができます。

※d:ピッチ円直径、z:歯数

※d:ピッチ円直径、z:歯数
上の2式によって、円ピッチは次式のように変形できます。
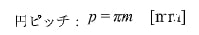
※m:モジュール
円ピッチから法線ピッチを、求めることができます。法線ピッチとは、基礎円においての円ピッチです。
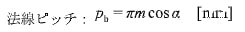
※m:モジュール、α:圧力角
この他、中心距離を算出します。中心距離とは、歯車同士の軸中心間の距離のことです。
中心距離は、かみ合うそれぞれの歯車の、基準ピッチ円の半径の和に等しい。したがって、以下の計算式のようになります。

※d:ピッチ円直径、m:モジュール、z:歯数
中心距離の精度が悪い場合、歯車の歯当たりが悪くなり、振動や騒音を発生しやすくなります。また、歯車の寿命も著しく低下します。このため、中心距離は、精度を重視して設計、加工、組み立てを行う必要があります。上記の内容も含めて、歯車の各寸法についてまとめたものを表2に示しています。

歯車の速度伝達比とは、駆動歯車の角速度と、被動歯車の角速度の比のことです。平歯車の場合、速度伝達比は次式のように示すことができます。
![※ω:角速度[rad/s]、n:回転数[min-1]、z:歯数](img/column/gear2/img_010.jpg)
※ω:角速度[rad/s]、n:回転数[min-1]、z:歯数
速度伝達比を設定すると、歯数を決定することができます。また、被動歯車での出力トルクは、入力トルクに速度伝達比の逆数をかけたものに等しいです。
かみ合い率とは、歯のかみ合っている対の数の平均値です。つまり、かみ合い長さを法線ピッチで割った値です。具体例としては、ε=1.5の場合は、少なくとも1歯は常にかみ合っており、かみ合い長さの始めと終わり0.5×法線ピッチの間は、2歯でかみ合っているということです。ε=2.4の場合には、少なくとも2歯は常にかみ合っており、かみ合い長さの、始めと終わり0.4×法線ピッチの間は、3歯かみ合っているということです。
1対の歯車が、連続的になめらかに回転するためには、歯の高さおよび歯すじの方向を適当にしなければなりません。平歯車では、はすば歯車のように、歯すじのねじれによってかみ合いをなめらかにすることは期待できないので、1対の歯形のかみ合いが終わらないうちに、つぎの1対の歯形がかみ合いに参加するようにするといいです。こうすることで、1歯でかみ合う場合よりも、2歯でかみ合う場合の方が、荷重が分散されますため、歯1枚あたりに加わる負担が軽減されます。通常はε=1.4からε=1.9とすることが多いです。かみ合い率の大きい方が、歯に加わる荷重の負担が少なくなり、歯車の伝動がなめらかになります。
このように、かみ合い率を算出することで、作用線上でどれだけの長さが1歯でかみ合い、どれだけの長さが、2歯でかみ合っているのかを、計算することができます。
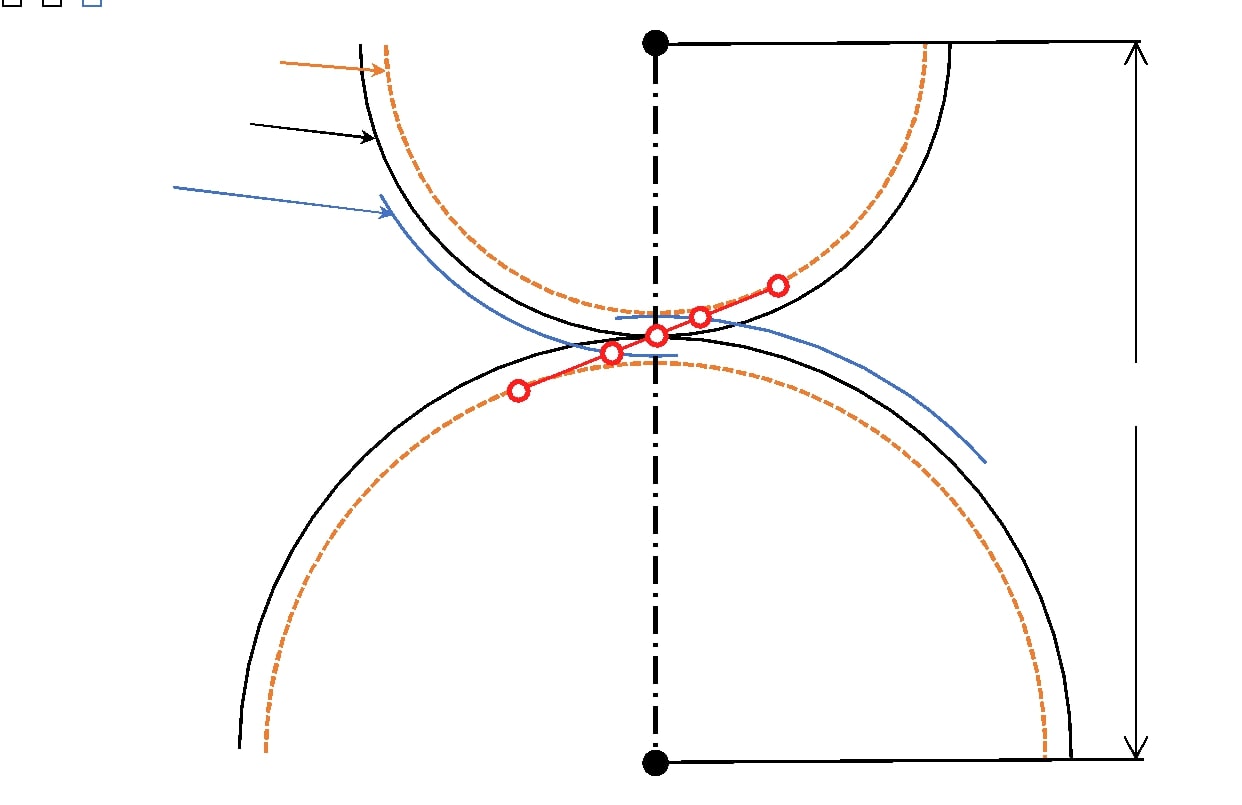
平歯車噛み合いの模式図
かみ合い率は、前述の通りかみ合い長さを法線ピッチで割った値に等しく、以下のように示すことができます。

※pb:法線ピッチ

これらの値は、後述するすべり率などでも必要となる値です。求める式をまとめたものを図にしました。
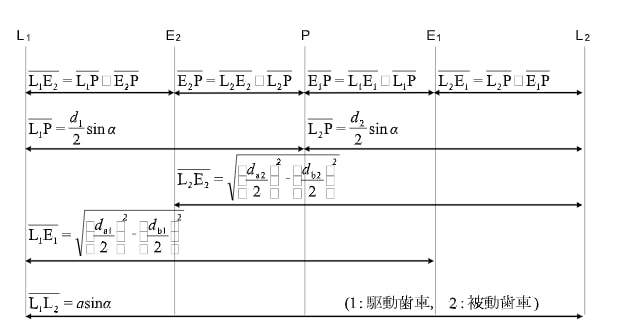
間の各長さ

歯面の損傷は、歯面の接触部におけるすべりの、大きさとその方向が非常に影響します。一般に、かみ合っている1対の歯の歯面は、かみ合いのピッチ点以外では必ずすべりが生じます。すべり率を定義することで、どれだけすべっているかを、計算することができます。すべり率は、互いの歯車の相対速度比から考えられたものです。任意の歯の接触点をQとおけば、次式のように示すことができます。Σ1が、駆動歯車に対してのすべり率、Σ2が被動歯車に対してのすべり率です。

※z:歯数
すべり率は、一般的にピッチ点においてはΣ=0になり、ここを離れるにしたがって変化します。

このことから、歯元付近の歯面は、すべり率が大きいために、よく摩耗することが考えられます。
すべり速度とは、駆動歯車と被動歯車の歯の相対速度です。すべり速度、Vg=0である場合、すべりは無い状態ですことを示しています。すべり速度を示すために、ピッチ点から接触点までの距離eを、定義します。

上式から、ピッチ点においては、e=0ですため、Vg=0となります。ピッチ点から離れるにしたがって、eの絶対値が大きくなるため、すべり速度も増大していきます。このため、すべり速度はかみ合い始めと終わりで最大となります。

弊チームマシン
いかがでしたでしょうか。今回は、前回よりも少し掘り下げ平歯車における諸計算式について紹介しました。これを機に、歯車について興味をもっていただけますと幸いです。
(横浜国立大学フォーミュラプロジェクト 駆動設計担当)
あわせて読みたい!お役立ちコラム